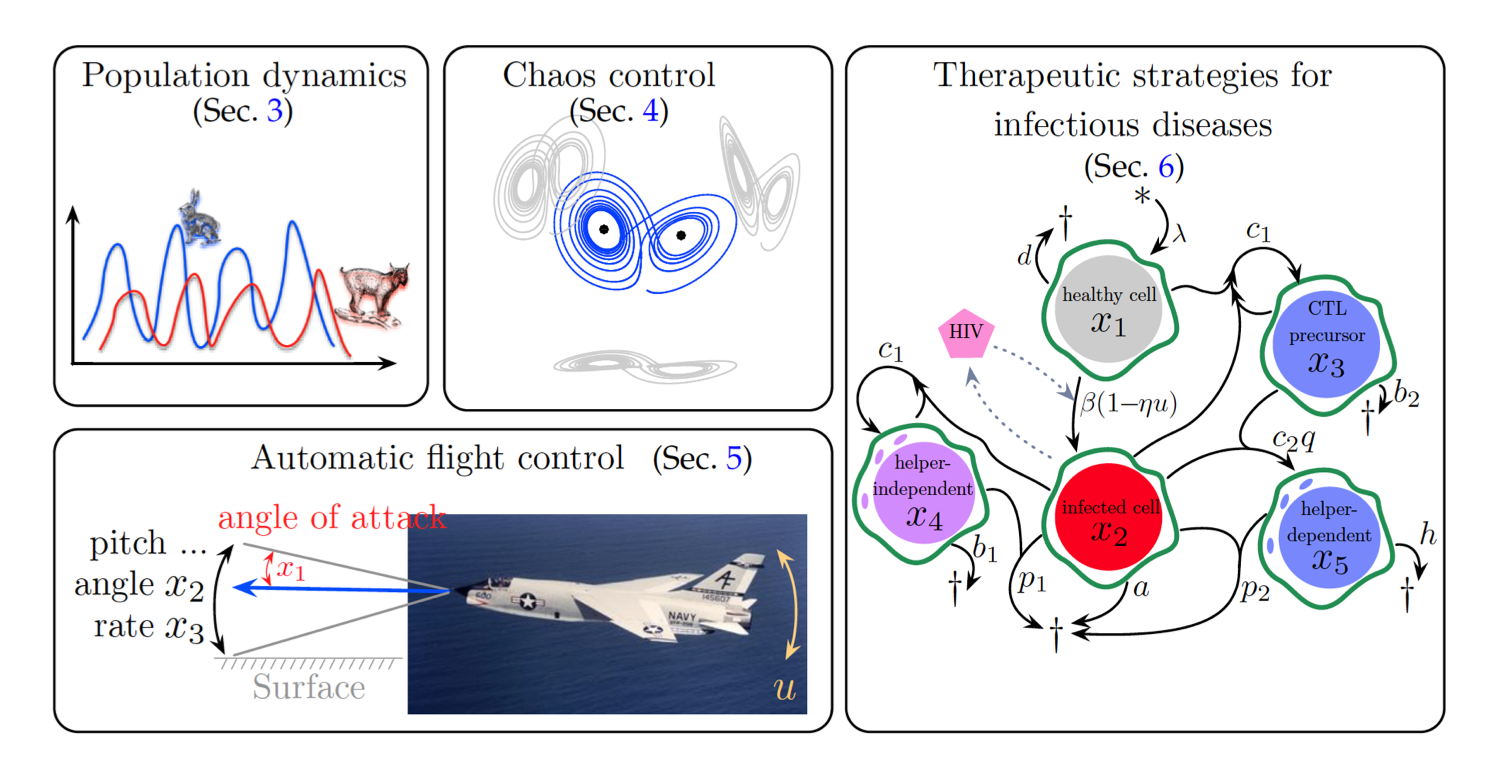
Research Projects

Operator-theoretic methods to model and control dynamical systems

Koopman and Perron-Frobenius operators are fundamentally changing how we approach dynamical systems, as these provide linear representations for even strongly nonlinear systems. In contrast to linear systems, a generally applicable and scalable framework for the control of nonlinear systems remains an engineering grand challenge. Improved nonlinear control has the potential to transform our ability to interact with and manipulate complex systems across broad scientific, technological, and industrial domains. From turbulence control to brain-machine interfaces, emerging technologies are characterized by high-dimensional, strongly nonlinear, and multiscale phenomena that lack simple models suitable for prediction and control design. This lack of simple equations motivates data-driven methodologies, which include system identification for model discovery.

Alternatively, one can seek transformations that embed nonlinear dynamics in a global linear representation, as in the Koopman framework. The goal of operator-theoretic frameworks is to reformulate nonlinear dynamics in a linear framework to enable the use of powerful linear methods for estimation, prediction, and control.

Discovery of laws of physics and control in the low-data limit

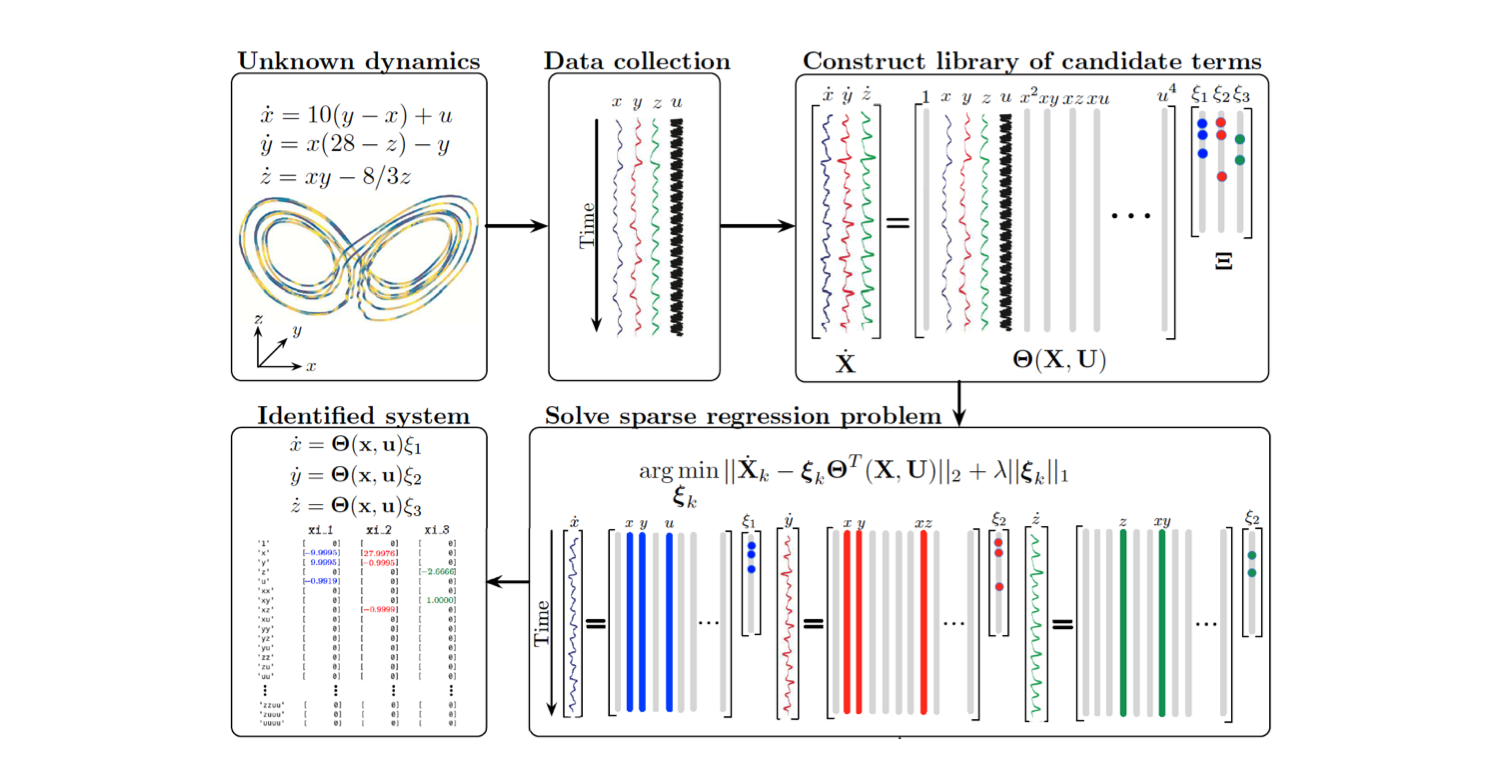
Data-driven discovery of dynamics via machine learning is pushing the frontiers of modeling and control efforts. However, many leading methods in machine learning, such as neural networks, require large volumes of training data, may not be interpretable, do not easily include known constraints and symmetries, and may not generalize beyond the attractor where models are trained. These factors limit, e.g., their use for the online identification of a model in the low-data limit, for example following an abrupt change to the system dynamics.

Building on recent work for the sparse identification of nonlinear dynamics (SINDy) modeling procedure, we use library construction and sparse regression to learn governing equations and conservation laws for control. In particular, parsimonious representations are learned, identifying the fewest terms in the model needed to explain the data, making them interpretable and generalizable. We further demonstrate that the discovered models enhance the performance of model predictive control (MPC). The resulting SINDYc-MPC framework requires significantly less data, and is more computationally efficient and robust to noise than neural network models, making it viable for online training and execution in response to rapid system changes. The approach is demonstrated on a variety of systems with different complexity and partial measurements.

Sensor placement informed by features and models

Efficient sensing is of great importance to
facilitate low-latency, fast-bandwidth data transmission and hyperreduction of data for improved storage and faster computations, particularly when processing massive amounts of data in real-time. However, optimal sensor selection is a NP-hard problem. One direction we pursue is centered around the observation that the representation of many systems is optimally sparse in an l2 coded basis (i.e., PCA, POD). In addition, it has been widely recognized that l1 penalizations in optimization problems promote sparsity.

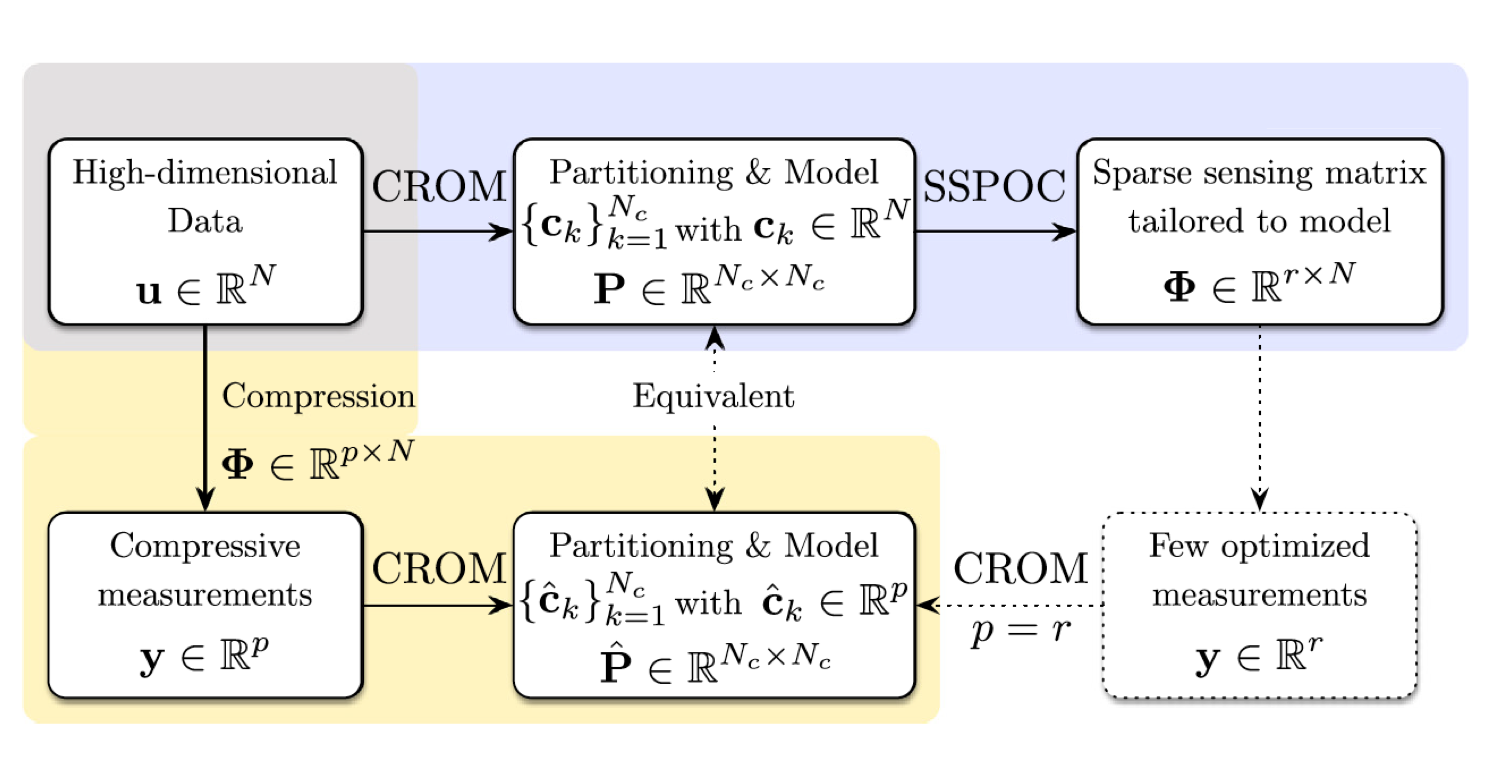
With that in mind, we combined the cluster-based reduced-order modeling (CROM) framework with sparsity-promoting and sparse sampling techniques (such as SSPOC and QR column pivoting) to estimate models from compressive or few, optimized measurements leveraging that in most systems the essential dynamics evolve on a low-dimensional attractor (Kaiser et al. J. Comp. Phys. 2017). We demonstrated that geometric properties of the partition and the probabilistic dynamics of the model are preserved and that significantly fewer sensors are required than using compressive sampling to inform categorical decision-making. This work enables further opportunities for partition-based modeling from few measurements and unsupervised optimal sensor placement for classification problems.

We also investigated the optimization of sensor placement informed by a library of spatiotemporal features, which are associated with transient and intermittent phenomena (Manohar et al. SIAM MMS 2019). This work was led by Krithika Manohar and combined multi-resolution dynamic mode decomposition (DMD) with sparse sampling for the diagnostic analysis of multiscale physics. Multiresolution DMD separates the dynamics into a hierarchy of components, where each level divides dynamics into slow and fast timescales. These multiresolution DMD modes can be used to determine sparse sampling locations which are nearly optimal for dynamic regime classification and full state reconstruction. It was demonstrated that only a small number of sensors are needed to accurately reconstruct the global temperature field and to classify El Ni~no events.

Cluster-based control for strongly nonlinear dynamics

Cluster-based coarse graining of state space has further led to model-based and model-free control approaches for strongly nonlinear dynamics. The partitioning of the high-dimensional state into few clusters enables an efficient discretization of a global control law.

One direction we pursue is a probabilistic model-based approach building on a cluster-based discretization of the Liouville equation for the evolution of the probability distribution (see e.g. CROM below). The control of the Liouville equation is a promising direction for systems that exhibit uncertainties in initial conditions and system parameters. The temporal evolution of the probability distribution on the set of clusters is then described by a control-dependent Markov model. This Markov model can be used as predictor for the ergodic probability distribution for a particular control law. This probability distribution approximates the long-term behavior of the original system on which basis the optimal control law is determined. This approach was demonstrated on a separating flow over a smoothly contoured wall to reduce the size of the recirculation area (Kaiser et al. TCFD 2017).

More recently, led by Aditya Nair, we developed a model-free self-learning cluster-based control strategy demonstrated on high-fidelity simulations of post-stall separated flows over an airfoil. Here, not the state is clustered but the aerodynamic forces providing a low-dimensional feature space. A feedback control law is then sought for each cluster state through iterative evaluation and downhill simplex search to minimize power consumption in flight (Nair et al. JFM 2019).

Low-dimensional statistical closure models for turbulence

In this project, we study the development of low-dimensional statistical closure models for turbulent flows using a data-driven approach. In the cluster-based reduced-order modeling (CROM)(Kaiser et al. JFM 2014) framework coarse-graining of the state space is combined with a statistical analysis to approximate the Liouville operator (the generator of the Perron-Frobenius operator) as a Markov model.

The data-driven discretization based on a clustering algorithm enables an efficient partitioning of the high-dimensional state space and scales with the dimension of the intrinsic dynamics instead of the spatial resolution. This approach represents a statistical closure model, but also enables broader applications, e.g. for optimizing PDE-based techniques which suffer from the curse of dimensionality. We have demonstrated CROM’s capabilities for the identification of physical mechanisms, principal dynamics, precursors and control laws in numerous fluid dynamical problems ranging from numerical simulations of the cylinder flow, mixing layer, bluff body flows (car and train models)(see, e.g., Kaiser et al. JFM 2014, Cao et al. Exp. Fl. 2014, Östh et al. JWEIA 2015) to experiments of an internal combustion engine, we have combined CROM with model selection using information measures for balancing model complexity, i.e. number of clusters, and with prediction accuracy, which was used to examine buffeting occurring at a space launcher (Loosen et al. 2017).